Given the following function:

Let's first spread the equation based on the exponents,
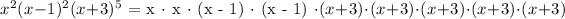
Let's then find the zeros of the factors,
x → x = 0
x → x = 0
x - 1 → x = 1
x - 1 → x = 1
x + 3 → x = -3
x + 3 → x = -3
x + 3 → x = -3
x + 3 → x = -3
x + 3 → x = -3
Therefore, the zeros are: 0, 0, +1, +1, -3, -3, -3, -3, -3
Let's now determine the multiplicity of multiple zeros,
0 mult. 2
+1 mult. 2
-3 mult. 5