Question

Kylie went to a store on three different days. She spent $6 on the first day, $14 on the second day, and x on the third day. If the mean amount that Kylie spent at the store was $16 per day, what is the value of x? O $10 O $16 O $22 O $28

Answer 1

We know that

• She spent $6 on the first day, $14 on the second day, and ,x, on the third day.

,

• The mean is $16 per day.

To solve this problem, we have to use the formula for the mean.

`\bar{x}=(\Sigma(x_i))/(N)`

In words, we have to sum all the money spent and then we divide it by the total number of days. Also, the mean is 16.

`16=(6+14+x)/(3)`

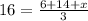
Now, we solve for x. First, we multiply each side by 3.

`\begin{gathered} 16\cdot3=(6+14+x)/(3)\cdot3 \\ 48=6+14+x \\ 48=20+x \end{gathered}`

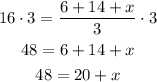
Then, we subtract 20 on each side.

`\begin{gathered} 48-20=20-20+x \\ x=28 \end{gathered}`

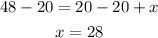
Therefore, the value of x is 28.