Given:
Nuts = $2.50
Cereal mixture = $1
Find -: How much each should be added.
Sol:
Obtain = 60 kg.
Let nuts = x kg
Cereal = y kg
To obtain 60 kg means:
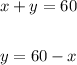
Pricing at $1.90 per kg means:
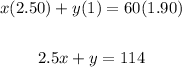
Put the value of "y" then:
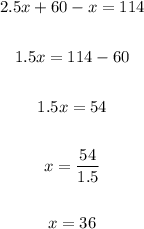
Then the value of "y" is:
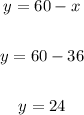
So,
In the mixture 36 kg of nuts and 24 kg of cereal.