Question

I need help with a homework problem, for both questions a & b.

Answer 1

- We need to find the Z-score that corresponds to the value of x = 208. After this, we can proceed to find the probability of getting a population greater than this value using Z-distribution tables or a Z-score calculator.

- The Z-score formula is:

`\begin{gathered} Z=(X-\mu)/((\sigma)/(√(n))) \\ where, \\ \sigma=\text{ The standard deviation} \\ \mu=\text{ The mean} \\ n=\text{ The number of data points in the sample} \end{gathered}`

- Thus, we can calculate the Z-score as follows:

`\begin{gathered} X=208,\mu=196.2,\sigma=31.7,n=30 \\ \text{ Thus, we have:} \\ \\ Z=(208-196.2)/((31.7)/(√(30))) \\ \\ Z=2.03884 \end{gathered}`

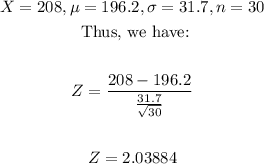
- Now, we can apply the Z-score calculator to convert the Z-score to a probability as follows:

- Thus, the probability of getting a population greater than 208 is 0.020733