The given exponential function is

Where x is the number of years after 1968
f(x) is the population in millions
a) Substitute x by 0
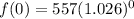
Since any number to the power of zero = 1, then
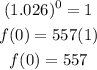
The population in 1968 is 557 million
b) At year, 2000 we need to find the value of x
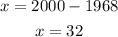
Now let us find f(32)
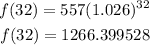
Round it to the nearest whole number
Then the population in 2000 is 1266 million