Question

Evaluate the expression:5^3.2 = y

Answer 1

Given the following expression:

`\text{ 5}^{3.2^{}}\text{ = y}`

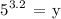
To expand the given exponential expression, we first convert 5.2 into an improper fraction.

We get,

`3.2\text{ = 3}(20)/(100)\text{ = 3}(1)/(5)`
`\text{ 3}(1)/(5)\text{ = }\frac{1\text{ + (3 x 5)}}{5}\text{ = }\frac{1\text{ + 15}}{5}`
`\text{ = }(16)/(5)`

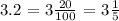
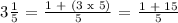
Reconstructing the expression, we get:

`\text{ 5}^(3.2)\text{ = y }\rightarrow5^{(16)/(5)}=\text{ y}`

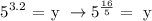
When the exponent is a fraction, the numerator remains the exponent of the base while the denominator becomes the degree of the root.

We get,

`\text{ 5}^{(16)/(5)}\text{ = y }\rightarrow\text{ }\sqrt[5]{5^(16)}\text{ = y}`