Given:
The equation is given as,
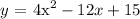
Required:
The number of x intercepts.
Step-by-step explanation:
On comparing the given equation with the standard form of the quadratic equation.
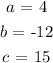
A number of x-intercepts refer to the number of roots of the given quadratic equation.
The discriminant of the given quadratic equation is calculated as,
