What is the transformation of g(x) = 4 - {x}^(3)

Question

What is the transformation of
`g(x) = 4 - {x}^(3)`

Answer 1

Given the transformed function:

`g(x)=4-x^3`

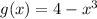
We want to describe the transformation with respect to the parent function:

`f(x)=x^3`

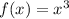
The "negative" in front of x^3 makes the graph reflect about x -axis.

Then, we have another transformation. There is a "+4" at the beginning.

This shifts the graph 4 units up.

Thus, the function f(x) is transformed to g(x) by:

• Shifting 4 units up

,

• being reflected about the x-axis

We can show the graph of both the functions.

`\begin{gathered} f(x)=x^3 \\ g(x)=4-x^3 \end{gathered}`

Parent function is the red one.

Transformed function, g(x), is the blue one.