First, let's expand the given equation:
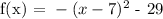
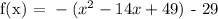
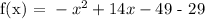

We get, a = -1, b = 14 and c= -78
A.) Let's determine the vertex.
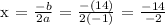
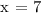
Substituting x = 7 in the equation, let's find y.

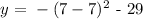
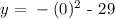
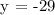
Therefore, the coordinate of the vertex is x,y = 7, -29
B. Let's determine the equation of the axis of symmetry.
The equation for the axis of symmetry of a parabola can be expressed as:

We get,
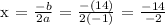
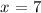
Therefore, the equation for the axis of symmetry is x = 7.