Question

Is (x+1) a factor of f(x) = x^4 - 3x^3 + 2x - 2?

Answer 1

`\text{Yes}`

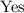
Step-by-step explanation:

According to the factor theorem, if we set x+1 to zero, the substitute the x value into the polynomial, if we get a value of zero, then x+1 is a factor of the polynomial, otherwise, it is not

We start by setting x+1 to zero:

`\begin{gathered} \text{ x+1 = 0} \\ x\text{ = -1} \end{gathered}`

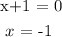
Substitute -1 into the polynomial:

`\begin{gathered} f(-1)=-1^4-3(-1)^3+2(-1)-2 \\ f(-1)\text{ = 1+3-2-2} \\ f(-1)\text{ = 4-4} \\ f(-1)\text{ = 0} \end{gathered}`

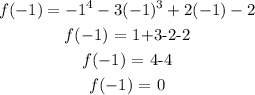
This shows that (x+1) is a factor of the polynomial