Question

Can a dividing function have an x intercept but not a y intercept?

Answer 1

A dividing function f(x) can be of the form:

`f(x)=(g\mleft(x\mright))/(h(x))`

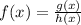
An x-intercept is where the function crosses the x-axis when plotted on a graph.

A y-intercept is where the function crosses the y-axis when plotted on a graph.

Therefore we can construct a dividing function that does cross the x-axis but not the y-axis.

This can be done by adding a constant to the function f(x) so as to shift it up or down, thereby crossing the x-axis

Let us take the function:

`f(x)=(1)/(x)`

as example.

This is plotted below:

As we can see, this graph does not cross either the x or y-axis.

But in order to make it cross the x-axis and hence have an x-intercept, we simply need to add a constant to the function.

We do this by:

`f(x)=(1)/(x)+4`

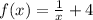
Plotting this new function, we have:

As we can see, because the graph has been shifted by the constant 4, the graph moves upwards, thereby making it cross the x-axis.

Therefore, the answer is True