Question

I need help with this practice problemStruggling to solve it

Answer 1

Let's start by sketching the triangle:

For the trignometric rates, we have:

`\begin{gathered} \sin \alpha=\frac{\text{opposite leg}}{\text{hypotenuse}} \\ \cos \alpha=\frac{\text{adjacent leg}}{\text{hypotenuse}} \\ \tan \alpha=\frac{\text{opposite leg}}{\text{adjacent leg}} \\ \sec \alpha=\frac{\text{hypotenuse}}{\text{adjacent leg}} \\ \csc \alpha=\frac{\text{hypotenuse}}{\text{opposite leg}} \\ \cot \alpha=\frac{\text{adjacent leg}}{\text{opposite leg}} \end{gathered}`

So firts, let's find the missing side using Pythagora's Theorem:

`\begin{gathered} FG^2+EF^2=EG^2 \\ 4^2+EF^2=10^2 \\ EF^2=100-16 \\ EF=\sqrt[]{84}=\sqrt[]{4\cdot21}=2\sqrt[]{21} \end{gathered}`

For E, the opposite leg is FG and the adjancet leg is EF, so:

`\cos E=(EF)/(EG)=\frac{2\sqrt[]{21}}{10}=\frac{\sqrt[]{21}}{5}`

For G, the opposite leg is EF and the adjacent leg is FG, so:

`\sec G=(EG)/(FG)=(10)/(4)=(5)/(2)`

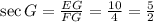
And:

`\tan G=(EF)/(FG)=\frac{2\sqrt[]{21}}{4}=\frac{\sqrt[]{21}}{2}`