To finsd the lengths in a plane, we can use the coordinates of the endpoints of the segment we want the length of.
Given the endpoitn, the distance between them is:
![d=\sqrt[]{(x_1-x_2)^2+(y_1-y_2)^2}](https://img.qammunity.org/2023/formulas/mathematics/college/87agft4bkj7u5ow4h8vn3yzn1g00q311fw.png)
For the length of MN, we ned to use the andpoints M and N, which are at coordinates:
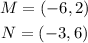
So, MN is:
![\begin{gathered} MN=\sqrt[]{(-6-(-3))^2+(2-6)^2} \\ MN=\sqrt[]{(-6+3)^2+(-4)^2} \\ MN=\sqrt[]{(-3)^2+16} \\ MN=\sqrt[]{9+16} \\ MN=\sqrt[]{25} \\ MN=5 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/k0pv6g0yupdkb17337k3tmg0y0wdzjqzzw.png)
Thus, the length of MN is 5.
For the length of MP, we have the points:
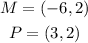
Thus:
![\begin{gathered} MP=\sqrt[]{(-6-3)^2+(2-2)^2} \\ MP=\sqrt[]{(-9)^2+(0)^2} \\ MP=\sqrt[]{81} \\ MP=9 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/tk2c7cemd6a2nafuni2cg4dsmetqpa91yg.png)
Thus, the length of MP is 9.
The perimeter of a figure is the sum of its sides, so it will be:
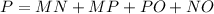
But opposite sides of a parallelogram are congruent, so:

Thus:
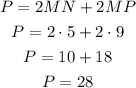
Thus, the perimeter is 28.