Question

Suppose x is any positive number. Circle 1 has a center at (1, −6) and a radius of 5x. Circle 2 has a center at (5, −1) and a radius of 3x. Why is Circle 1 similar to Circle 2? Circle 1 is a translation of 4 units left and 5 units down from Circle 2, and a dilation of Circle 2 with a scale factor of 53. Circle 1 and Circle 2 have the same area, and the radius of Circle 1 is53 times the length of Circle 2's radius. Circle 1 and Circle 2 have the same circumference, and the radius of Circle 1 is35 times the length of the radius of Circle 2. Circle 1 is a translation of 4 units left and 5 units down from Circle 2, and a dilation of Circle 2 with a scale factor of 35.

Answer 1

- We can plot the graphs of both circles to compare them.

- This is done using a graphing calculator, shown below:

- We can see that circle 1 is bigger than circle 2. Thus, the area of circle 1 is larger than the area of circle 2 and the circumference of circle 1 is also larger than the area of circle 2.

- This implies that Option 2 and 3 are incorrect.

- The circle 1 is a dilation of circle 2, thus, we can say:

`sf=(r_1)/(r_2)=\frac{radius\text{ of circle 1}}{radius\text{ of circle 2}}`

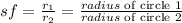
- If the radius of circle 1 is 5x, and the radius of circle 2 is 3x, the scale factor is

`sf=(5x)/(3x)=(5)/(3)`

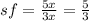
Final answer

The answer is Option 1