Answer:
The given binomial(x + 9) is a factor of the given polynomial by Factor Theorem
Step-by-step explanation:
Given the below polynomial;
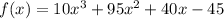
We're asked to state if the binomial (x + 9) is a factor of the above polynomial.
To do that, we have to apply the Factor Theorem, which states that if f(x) is a polynomial function, then (x - c) is a factor of f(x) if and only if f(c) = 0.
So let's go ahead and determine f(-9);
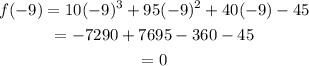
Since f(-9) is 0, therefore by Factor Theorem, (x + 9) is a factor of the polynomial.