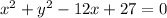Question

Which of the following equations represents the equation of the circle below ?

Answer 1

Given the graph of a circle

To find the equation of the circle, we need to find the location of the center and the length of the radius

As shown, we can notice that the x-axis bisect the circle

So, the diameter and the center are lying on the x-axis

The diameter is the length between the points of intersection with the x-axis

As shown, the diameter is the line segment with the endpoints:

(3, 0) and (9, 0)

so, the diameter = 9 - 3 = 6

So, the radius = r = 3

And the location of the center = (h, k) = (6, 0)

The equation of the circle will be as follows:

`\begin{gathered} (x-h)^2+(y-k)^2=r^2 \\ (x-6)^2+(y-0)^2=3^2 \end{gathered}`

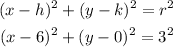
Expand then simplify:

`\begin{gathered} x^2-12x+36+y^2=9 \\ \\ x^2+y^2-12x+27=0 \end{gathered}`

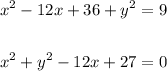
So, the answer will be option 3

`x^2+y^2-12x+27=0`