Step-by-step explanation
We are told that the weight of an object varies directly with the mass of the object. This basically means that if w is the weight and M is the mass then these two magnitudes are related by the following expression:
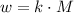
Where k is a constant.
We know that an object with a mass of 80kg weights 80 newtons. Then for this object we have w=80kg and M=80n so we get:
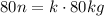
We divide both sides of this equation by 80:

Here it's important to remember that 1 newton (i.e. 1n) is equal to:
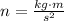
Then we get:

We divide both sides by 1 kg:
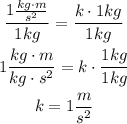
So now that we found k we have the following expression for the weight of an object as a function of its mass:
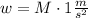
For an object that weights 70n we get:
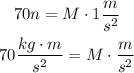
We divide both sides by 1 m/s²:
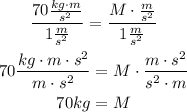
Answer
So the mass of an object that weights 70n is 70kg.