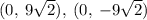Solution:
The standard equation of a hyperbola is expressed as
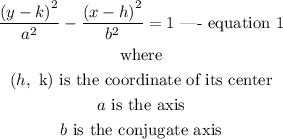
Given the equation of the hyperbola to be
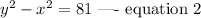
Express equation 2 in a similar form as equation 1.
Thus,
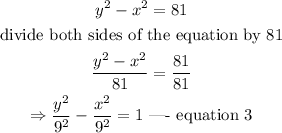
In comparison with equation 1, we can conclude that
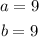
Vertices of the hyperbola:
The vertices of the hyperbola are expressed as
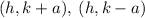
where
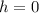
The vertices of the hyperbola are evaluated to be
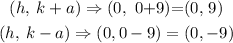
Hence, the vertices of the hyperbola are
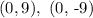
Foci of the hyperbola:
The foci of the hyperbola are expressed as
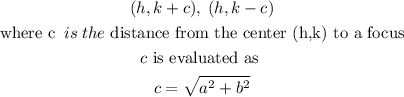
Evaluating c gives
![\begin{gathered} c=√(a^2+b^2) \\ =\sqrt[]{9^2+9^2} \\ =\sqrt[]{81+81} \\ =\sqrt[]{162} \\ c=9\sqrt[]{2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/86v2c5fit3hs5o3tf1aeq2l5ww1zmt2wxx.png)
Thus, the foci are evaluated as
![\begin{gathered} (h,k+c)\Rightarrow(0,\text{ 0+9}\sqrt[]{2})=(0,9\sqrt[]{2}) \\ (h,k-c)\Rightarrow(0,\text{ 0-9}\sqrt[]{2})=(0,-9\sqrt[]{2)} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/3oaroxxxdut69813rws7whusy6v1spv7yd.png)
Hence, the foci of the hyperbola are