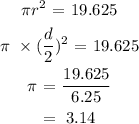Question

Circle A has a diameter of 9 inches, a circumference of 28.26 inches, and an area of 63.585 square inches. The diameter of circle B is 5 inches, The circumference is 15.70 inches and the area is 19.625Part A: using the formula for circumference, solve for the value of pi for each circlePart B: use the formula for area to solve for the value of pi for each circle

Answer 1

Given:

The parameters for circle A:

diameter = 9 inches

circumference = 28.26 inches

area = 63.585 square inches

The parameters for circle B:

diameter = 5 inches

circumference = 15.70 inches

area = 19.625 square inches

The formulas for the area and circumference of a circle:

`\begin{gathered} \text{Circumference of a circle = 2}\pi r \\ \text{Area of a circle = }\pi r^2 \end{gathered}`

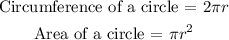
Part A

Using the formulas, we can solve for pi for each cicle:

Circle A:

`\begin{gathered} 2\pi r\text{ = 28.26} \\ \pi d\text{ = 28.26} \\ \pi\text{ }*\text{ 9 = 28.26} \\ \text{Divide both sides by 9} \\ \pi\text{ = 3.14} \end{gathered}`

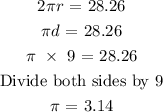
Circle B:

`\begin{gathered} 2\pi r\text{ = }15.70 \\ \pi d\text{ = 15.70} \\ \pi\text{ }*\text{ 5 = 15.70} \\ \text{Divide both sides by 5} \\ \pi\text{ = 3.14} \end{gathered}`

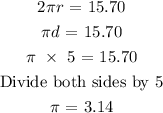
Part B:

Circle A:

`\begin{gathered} \pi r^2\text{ = 63.585} \\ \pi\text{ }*((d)/(2))^2\text{ = 63.585} \\ \pi\text{ }*20.25\text{ = 63.585} \\ \pi\text{ = 3.14} \end{gathered}`

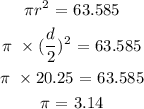
Circle B:

`\begin{gathered} \pi r^2\text{ = }19.625 \\ \pi\text{ }*((d)/(2))^2\text{ = 19.625} \\ \pi\text{ = }(19.625)/(6.25) \\ =\text{ 3.14} \end{gathered}`