Question

Graph the piecewise function f(x) = 3/2x+1 , -4 <= x<= 0 x-5 , 1 <= x<= 3 The image is attached for reference.

Answer 1

The piecewise function f(x) is composed bt two lines: 3/2x + 1 and x - 5. To graph a line, we need to connect two points that lie on the line. In the case of the first line, we can use its endpoints x = -4 and x = 0.

Substituting x = -4 into the equation of the first line, we get:

`\begin{gathered} y=(3)/(2)(-4)+1 \\ y=-6+1 \\ y=-5 \end{gathered}`

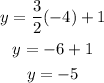
Then, the point (-4, -5) lies on the first line.

Substituting x = 0 into the equation of the first line, we get:

`\begin{gathered} y=(3)/(2)(0)+1 \\ y=1 \end{gathered}`

Then, the point (0,1) lies on the first line.

In the case of the second line, the endpoints x = 1 and x = 3.

Substituting x = 1 into the equation of the second line, we get:

`\begin{gathered} y=1-5 \\ y=-4 \end{gathered}`

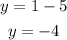
Then, the point (1,-4) lies on the second line.

Substituting x = 3 into the equation of the second line, we get:

`\begin{gathered} y=3-5 \\ y=-2 \end{gathered}`

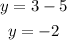
Then, the point (3,-2) lies on the second line.

Connecting these points with two different lines as stated before, we get the graph of f(x) as follows: