Question

I need help with my geometry homework.it is talking about inductive reasoning and logic symbols hw

Answer 1

So we need to take the expressions written with logical symbols and write them as compound statement. Then we must find their thruth value which basically means that we have to tell if they are true or false.

The first one is:

`p\lor q`

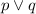
This is called a disjunction and can be described with the word "or". So considering what the statements p and q are the compund statement would be:

`p\lor q\colon\text{ Points C, E and }B\text{ are collinear or }\angle AEC\cong\angle DEB`

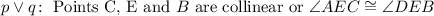
This is the first compound statement, we just need to find if its true or false. Since what we have is a disjunction then if both p and q are true, the statement is true. Also, if only one of them is true the statement is still true. A disjunction like this can only be false if both statement are false so let's check which is the case.

The first part, statement p is "Points C, E and B are collinear". Being collinear means that they all three share the same line. As you can see this is not true.

The second part is statement q and says that:

`q\colon\angle AEC\cong\angle DEB`

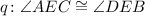
If you look carefully, you can see that angles AEC and DEB are defined by the same lines, share the same vertex and are opposite. All these means that in deed AEC and DEB have the same measure which means that this statement is true. So from the two statements that form the compund statement p v q one is true which means that the truth value of this one is True.

And that's the solution for number 1. Let's see number 2, we have:

`q\wedge s`

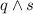
This is called a conjuction and can be expressed with the word "and". Then:

`q\wedge s\colon\angle AEC\cong\angle DEB\text{ and }\angle BEC\text{ is an acute angle}`

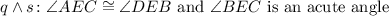
For conjuction, their truth value is true if both statements are true. In any other case, the truth value is false. So let's see, we have already found that statement q is true. We have to see what happens with statement s:

`s\colon\angle BEC\text{ is an acute angle}`

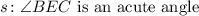
An acute angle is an angle whose measure is smaller than 90°. As you can see, BEC has to measure more than 90° since a 90° angle is made by two perpendicular sides. This means that statement s is false. Since both q and s are true then the Truth value of q ^ s is False.

Now in number 3 we have:

`\text{ \textasciitilde}p\wedge r`

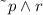
This is also a conjuction (we'll use the word "and") but this time there's a symbol ~ before p. In logical terms ~p is the statement that is exactly the opposite of p. So if p is "Points C, E and B are collinear" then ~p is "Points C, E and B aren't collinear". Another thing to notice is that if p is false then ~p has to be true. Now that we know this let's write the compound statement:

`\text{ \textasciitilde}p\wedge r\colon\text{Points C, E and }B\text{ aren't collinear and }EF\text{ is the angle bisector of }\angle AED`

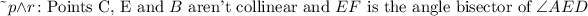
And let's find the truth value. As I said, if p is false then ~p is true so we just need to see if r is true or false. The angle bisector is a line or segment that "cuts" an angle through the middel. As you can see on the image EF does exactly this so statement r is true. So we have a conjuction of two true statements so the truth value is True.

In 4 we have:

`r\lor\text{ \textasciitilde}s`

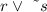
This is a disjunction so we have to use the word "or" and ~s is the opposite or the negation of s so we have that the compound statement is:

`r\lor\text{ \textasciitilde}s\colon EF\text{ is the angle bisector of }\angle AED\text{ or }\angle BEC\text{ isn't an acute angle}`

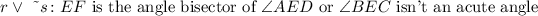
As we already saw before, r is a true statement and ~s is also true because s is false. This means that the truth value in this case is True.

In the last one we have:

`\text{ \textasciitilde}q\wedge\text{ \textasciitilde}r`

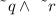
So we have a conjuction. This means that the compound statement is given by joining the negation of q with that of r with the word "and" between them:

`\text{ \textasciitilde}q\wedge\text{ \textasciitilde}r\colon\angle AEC\\e\angle DEB\text{ and }EF\text{ isn't the angle bisector of }\angle AED`

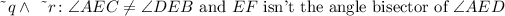
As we saw before, q and r are true so both ~q and ~r are false and the truth value is False.