We can draw the isosceles trapezoid as follows:
Then, the area of this isosceles trapezoid will be:
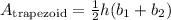
However, we need to find the height of the isosceles trapezoid, h, using the Pythagorean Theorem as follows:
Therefore, we can find, h, as follows:
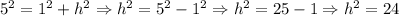
![h=\sqrt[]{24}\Rightarrow24=2^2\cdot2\cdot3\Rightarrow h=\sqrt[]{2^2\cdot6}\Rightarrow h=2\cdot\sqrt[]{6}](https://img.qammunity.org/2023/formulas/mathematics/college/ofzafkqfev5894zz28fvh0pvuo0vyd0hu9.png)
Then, the area of the isosceles trapezoid using the formula above as follows:
![A_{\text{trapezoid}}=(1)/(2)h(b_1+b_2)\Rightarrow\begin{cases}h=2\cdot\sqrt[]{6} \\ b_1=6 \\ b_2=8\end{cases}](https://img.qammunity.org/2023/formulas/mathematics/college/kx7b4dzjm0tmps9wil554x5s58mpovtdni.png)
Then, we have:
![A_{\text{trapezoid}}=(1)/(2)2\cdot\sqrt[]{6}(6+8)=14\cdot\sqrt[]{6}](https://img.qammunity.org/2023/formulas/mathematics/college/ld1poprovnr1o161hijdxby1j67wbdce5n.png)
In summary, the area of an isosceles trapezoid is (in square units):
![A_{\text{trapezoid}}=14\cdot\sqrt[]{6}](https://img.qammunity.org/2023/formulas/mathematics/college/e43z3y5dezkl72c7lr37q1hlcilcnidfxb.png)