Given:
probability = p = 0.75
sample size = no. of peas = n = 20
A.) The mean of a binomial distribution is the product of the sample size n and the probability p.
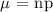
We get,
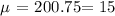
Therefore, the mean is 15.
B.) The standard deviation of a binomial distribution is the square root of the product of the sample size, n, and the probability, p.
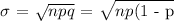
We get,
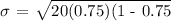
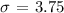
Therefore, the standard deviation is 3.75