Question

Given a circle with a center at (4.0) and a radius of 3, is the point (1,0) inside, outsideor on?

Answer 1

Consider that the equation of a ciircle with center (h,k) and radius 'r' is given by,

`(x-h)^2+(y-k)^2=r^2`

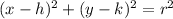
According to the given problem, the center is (4,0) and the radius is 3 units,

`\begin{gathered} (h,k)\equiv(4,0) \\ r=3 \end{gathered}`

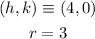
So the equation of this circle will be,

`\begin{gathered} (x-4)^2+(y-0)^2=3^2 \\ (x-4)^2+y^2=9 \end{gathered}`

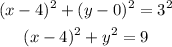
In this equation (x,y) are the coordinates of the points lying on the circle.

The left hand side (LHS) expression and right hand side (RHS) expression are,

`\begin{gathered} LHS=(x-4)^2+y^2 \\ RHS=9 \end{gathered}`

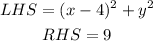
Now, consider the point (1,0). Substitute the values in RHS,

`\begin{gathered} LHS=(1-4)^2+0^2 \\ LHS=(-3)^2+0 \\ LHS=9 \\ LHS=RHS \end{gathered}`

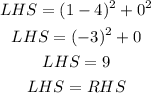
It is found that the point (1,0) satisfirs the equation of the circle. So it must lie on the periphery of the circle.

Thus, it can be concluded that point (1,0) lies on the circle.