Answer:
257.2 square inches
Step-by-step explanation:
Given the three sides of a triangle, the area is found using Heron's formula:
![\begin{gathered} \text{Area}=\sqrt[]{s(s-p)(s-q)(s-r)} \\ \text{Where p,q,r are the side lengths} \\ s=(p+q+r)/(2) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/1vfizosktwneuv4kevcdyq6rps9r3s9lqs.png)
First, find the value of s:
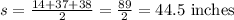
Next, substitute the values into the formula:
![\begin{gathered} \text{Area}=\sqrt[]{s(s-p)(s-q)(s-r)} \\ =\sqrt[]{44.5(44.5-14)(44.5-37)(44.5-38)} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/65l0qtdwyu87zo63bdtczdmc9mmllmjoh7.png)
Finally, simplify:
![\begin{gathered} =\sqrt[]{44.5(30.5)(7.5)(6.5)} \\ =\sqrt[]{66165.9375} \\ =257.23 \\ \approx257.2\text{ square inches} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/io5ddlysfvczpdmwb9sfrjwuktq6zlmzbk.png)
The area of triangle PQR is 257.2 square inches (to the nearest 10th of a square inch).