Question

(A) Find the marginal cost at a production level of a golf clubs.C'(x) =(B) Find the marginal cost of producing 55 golf clubs.Marginal cost for 55 clubs =

Answer 1

The marginal cost for producing 55 golf clubs is $31

Explanation:

Given information

`The\text{ total cost }in\text{ dollars = }550\text{ + 130x - }0.9x^2`

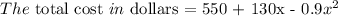
The next step is to find the marginal cost

The formula for finding marginal cost is given below as

`MC\text{ = }\frac{\text{ }\Delta C}{\text{ }\Delta x}`

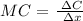
To find the marginal cost, we need to differentiate the total cost with respect to x

`\begin{gathered} MC\text{ = }\frac{\text{ }\Delta C}{\text{ }\Delta x}\text{ = C'(x)} \\ C^(\prime)(x)\text{ = 0 + 1 }*130x^{1\text{ - 1}}-2(0.9)x^{2\text{ -1}} \\ C^(\prime)(x)\text{ = 0 + 130 - 1.8x} \end{gathered}`

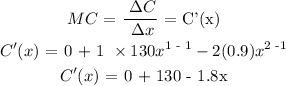
Therefore, the marginal cost is

`C^(\prime)(x)\text{ = 130 - 1.8x}`

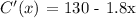
Part b

Find the marginal cost of producing 55 golf clubs

Let x = 55

The next step is to substitute the value of x = 55 into the above marginal cost formula

`\begin{gathered} C^(\prime)(x)\text{ = 130 - 1.8x} \\ C^(\prime)(55)\text{ = 130 - 1.8(55)} \\ C^(\prime)(55)\text{ = 1}30\text{ - 99} \\ C^(\prime)(55)\text{ = \$31} \end{gathered}`

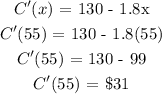
Therefore, the marginal cost for producing 55 golf clubs is $31