Question

Aө21 cmB25 cmWhat is the measure of ZA, to the nearest degree?sin AoppositehypotenuseCOS Aadjacenthypotenusetan Aoppositeadjacent404950

Answer 1

Given:

AB = 21 cm

BC = 25 cm

∠A = θ

Let's find the measure of angle A.

To find the measure of angle A, apply the trigonometric ratio for tan.

We have:

`\tan \theta=\frac{opposite}{\text{adjacent}}`

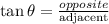
Where:

Opposite side is the side opposite the given angle(θ) = BC = 25 cm

Adjacent side is the side adjacent to the given angle (θ) = AB = 21 cm

Thus, we have:

`\text{tan}\theta=(25)/(21)`

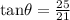
Solving further:

Take the inverse tangent of both sides

`\begin{gathered} \theta=\tan ^(-1)((25)/(21)) \\ \\ \theta=\tan ^(-1)(1.19) \\ \\ \theta=49.9\degree\approx50\degree \end{gathered}`

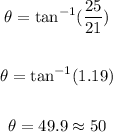
Therefore, the measure of ∠A to the nearest degree is 50°

ANSWER:

50°