Question

15. Your class rank in 2018 was 78 out of 456 students. In 2019 your class rank was 67 outof 501 students.a. In which year did you have the higher percentile ranking.b. If you had the data on the cumulative GPA of each student at the end of thespring semester in 2018, which measure of average would be the mostmeaningful – mean, median, mode? Explain.

Answer 1

The rankings are:

2018: 78 out of 456

2019: 67 out of 501

The rank and the percentile are related by:

`P=(i\cdot n)/(100)`

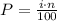
Where P is the position in the ranking, i is the percentile "type", and n is the number of students.

a)

Using the previous formula:

`\begin{gathered} 2018\colon78=(i\cdot456)/(100)\Rightarrow i=(78\cdot100)/(456)=17.1\text{\%} \\ 2019\colon67=(i\cdot501)/(100)\Rightarrow i=(67\cdot100)/(501)=13.4\text{\%} \end{gathered}`

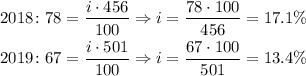
Since in this case the lower the rank, the higher the number. For example, rank 18 is higher than rank 400. Then, in this case, we use the complement to find the real percentile rank:

`\begin{gathered} 2018\colon100\text{\% }-17.1\text{\% }=82.9\text{\%} \\ 2019\colon100\text{\% }-13.4\text{\% }=86.6\text{\%} \end{gathered}`

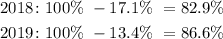
Then, the higher percentile ranking corresponds to 2019.

b)

If we have the cumulative GPA (grade point average), the mode is just the highest frequency of the distribution. The median is just the measure of cumulative GPA such that:

"50% of the students have a cumulative GPA of (median) or less"

The mean is just the average of all the distribution. Since the cumulative GPA is a measure that goes from 0 to 5, we can say that its distribution is somewhat normal, so the most meaningful measure of a normal distribution is the mean.