Question

you spin the spinner twice what is the probability of landing on a number less than eight and then landing on a 6

Answer 1

The probability of 2 consecutive events is the product of the probabilities of the single events.

The probability (P) of a single event A is:

`P(A)=\frac{number\text{ }of\text{ }favorable\text{ }outcomes}{t=number\text{ }of\text{ total }outcomes}`

So, let's find the probability of the first event:

Event: Landing on a number less than 6.

Number of Favorable outcomes: 2 (Landing on 6 or 7).

Total outcomes: 3 (Landing on 6, 7, or 8).

Then,

`P(A)=(2)/(3)`

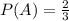
Now, let's find the probability of the second outcome:

Number of Favorable outcomes: 1 (Landing on 6 ).

Total outcomes: 3 (Landing on 6, 7, or 8).

`P(B)=(1)/(3)`

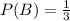
Then, the probability of landing on a number less than eight and then landing on a 6 ​is:

`\begin{gathered} P=P(A)*P(B) \\ P=(2)/(3)*(1)/(3) \\ P=(2)/(9) \end{gathered}`

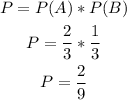
Answer: 2/9.