Step-by-step explanation:
Let the point (x,y) = (3,9) and the inequality y<16−x. If the point (x,y) is a solution to this inequality then replacing the coordinates of the point (x,y) on the inequality, the inequality would be true. Let's check this:
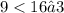
this is equivalent to saying:
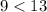
this is true, thus (3,9) is a solution to y<16−x.
Similarly consider the point (4,11) and the inequality y≤14−x. Thus:
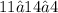
this is equivalent to:
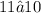
this is a contradiction, so we can conclude that the point (4,11) is not a solution to y≤14−x.
Now, consider the point (5,10) and the inequality y>15−x. Then:
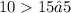
this is equivalent to:
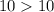
this is a contradiction, so we can conclude that the point (5,10) is not a solution to y>15−x.
Finally, consider the point (6,15) and the inequality y≥16−x. Then:
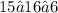
this is equivalent to:
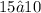
this is true, thus (6,15) is a solution to y≥16−x.
We can conclude that the correct answer is:
Answer:
a) (3,9) is a solution to y<16−x.
b) (4,11) is not a solution to y≤14−x.
c) (5,10) is not a solution to y>15−x.
d) (6,15) is a solution to y≥16−x.