Answer:
No solution
Step-by-step explanation:
The equation
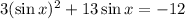
looks very much like a quadratic equation. Therefore, for the moment we say that
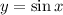
and write the above equation as
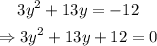
Using the quadratic formula, we find that the solutions to the above equation are given by
![y=\frac{-13\pm\sqrt[]{13^2-4(3)(12)}}{2\cdot3}](https://img.qammunity.org/2023/formulas/mathematics/college/midhdblwnobhitoscbq2x3y60egkmqze9l.png)
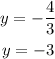
Reminding ourselves that actually y was sin(x) gives
![undefined]()