Question

Find the minimum or maximum of the quadratic function given below by completing the square. = -12 + 8r - 9 9 OA. Minimum at 25 ОВ. Maximum at -25 OC. Maximum at 7 OD Minimum at 7

Answer 1

Maximum at 7

Step-by-step explanation

By completing the square we will rewrite the equation in the form,

`f(x)=a(x-h)^2+k`

Where (h, k) is the vertex of the parabola - in other words, it is the maximum or minimum of the function.

To complete the square we have to find a perfect square, which has the form,

`(a+b)^2=a^2+2ab+b^2`

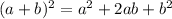
In the given function a = x, so the first term is x². However, in the given function the first term is negative, so we have to take -1 as a common factor first,

`f(x)=-(x^2-8x+9)`

The second term is -8x, so we can find b,

`\begin{gathered} 2ab=-8x \\ if\text{ a = x} \\ 2xb=-8x\Rightarrow b=-4 \end{gathered}`

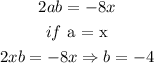
The perfect square should be,

`(x-4)^2=x^2-8x+16`

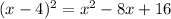
To have the same equation we have to subtract 16 and add 16 to the function,

`f(x)=-(x^2-8x+16-16+9)=-((x-4)^2-16+9)=-((x-4)^2-7)=-(x-4)^2+7`

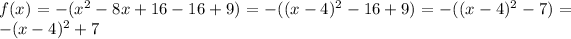
The vertex of the parabola is (4, 7). Hence, the maximum is at 7.

We know that it is a maximum because the coefficient a is negative, so the branches of the parabola point downward.