Question

Use the value of the discriminant to determine the number and type of roots for each equation.X^2=4x-4

Answer 1

The first step we have to follow is to write the equation in standard form:

`\begin{gathered} x{}^2=4x-4 \\ x^2-4x+4=0 \end{gathered}`

The discriminant of a quadratic expression is given by:

`D=b^2-4ac`

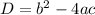
If the discriminant is greater than 0 and has a rational square root, the equation has 2 real rational roots; if it is greater than 0 and does not have a rational square root, the equation has 2 real irrational roots; if it is equal to 0, the equation only has 1 real rational root; and if it is less than 0, the equation has no real roots.

Find the discriminant using the values of the equation:

`\begin{gathered} D=(-4)^2-4(1)(4) \\ D=16-16 \\ D=0 \end{gathered}`

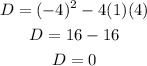
It means that this equation has 1 real, rational root.