Question

Find the interquartile range of the data set:4,15,17,18,20,21,23,25

Answer 1

6

Step-by-step explanation:

First, ensure the numbers are ordered in ascending order:

`4,15,17,18,20,21,23,25`

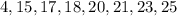
Since we have an even number of items, divide the items into two equal parts:

`(4,15,17,18,)(20,21,23,25)`

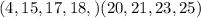
For the lower quartile, find the median of the lower half:

`Q_1=(15+17)/(2)=(32)/(2)=16`

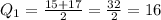
For the upper quartile, find the median of the upper half:

`Q_3=(21+23)/(2)=(44)/(2)=22`

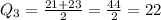
Finally, find the interquartile range:

`\begin{gathered} \text{IQR}=Q_3-Q_1 \\ =22-16 \\ =6 \end{gathered}`

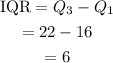
The interquartile range for the data set is 6.