Given:
There are given two triangles, ABC and DEF.
Where,
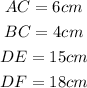
Step-by-step explanation:
To find the value of two congruent triangles, we need to use the ratio properties:
So,
From the given congruent triangle:
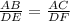
Then,
Put the all values into the above ratio expression:
So,
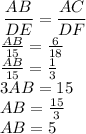
Final answer:
Hence, the correct option is D.