Question

This is called angle relationships and with triangles. Please help

Answer 1

`\begin{gathered} x=6 \\ m\angle STW=91^(\circ) \end{gathered}`

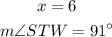
1) Note that there is a theorem of the External Angle that states its measure is equal to the sum of two remote angles inside a triangle.

2) So, we can write out the following equation and solve it for x:

`\begin{gathered} 14x+17=44+9x+3 \\ 14x-9x=44+3-17 \\ 5x=47-17 \\ 5x=30 \\ (5x)/(5)=(30)/(5) \\ x=6 \end{gathered}`

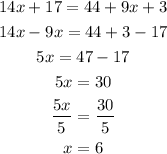
Now, we can plug into the expression that states the measure of angle ∠STW and find out the unknown measure:

`\begin{gathered} m\angle STW=14x+7,m\angle STW=14(6)+7=91^(\circ) \\ \end{gathered}`

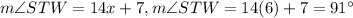
Thus, this is the answer.