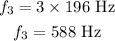Question

I don't know how to start. I attached the picture. can someone help?

Answer 1

Given data:

Frequency of fundamental harmonics, f = 196 Hz

Length of string, L = 0.34 m

Linear mass density of string,

`\mu=4*10^(-3)\text{ kg/m}`

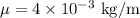
Formula of frequency of standing wave on a string is as follows:

`f_1=\frac{\sqrt[]{(T)/(\mu)}}{2L}`

Substitute given values in above equation,

`196=\frac{\sqrt[]{(T)/(4*10^(-3))}}{2*0.34}`

Taking square of above equation,

`\begin{gathered} 52245.76=(T)/(4*10^(-3)) \\ T=208.98\text{ N} \end{gathered}`

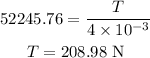
Formula of velocity is as follows:

`v=\sqrt[]{(T)/(\mu)}`

Here, T is tension

Substitute known values in above equation,

`\begin{gathered} v=\sqrt[]{(208.98)/(4*10^(-3))} \\ v=\sqrt[]{52245} \\ v=228.57\text{ m/s} \end{gathered}`

Formula of frequency of nth harmonics is as follows:

`f_n=nf_1`

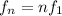
Now, In the given case,

we have to find frequency of first three harmonics

Frequency of fundamental harmonics is given.

Hence,

Frequency of second harmonics is as follows:

Substitute values of frequency fundamental harmonics in above equation,

`\begin{gathered} f_2=2*196\text{ Hz} \\ f_2=392\text{ Hz} \end{gathered}`

Frequency of third harmonics is as follows:

`\begin{gathered} f_3=3*196\text{ Hz} \\ f_3=588\text{ Hz} \end{gathered}`