We are asked to determine the equation of a line that passes through the point (12, -5) and slope -1. To do that let's remember that the general form of a line equation is the following:

Where "m" is the slope and "b" the y-intercept. Replacing the value of the slope we get:
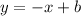
To determine the value of the y-intercept we need to replace the point (12, -5), this means that when x = 12, y = -5:
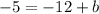
Now we solve for "b" by adding 12 to both sides:
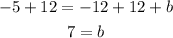
Replacing the value of "b" we get the equation of the line:
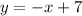
To do the graph of this line we need two points that are in the line. The first point can be the y-intercept since that is equivalent to the point (0, 7). The second point can be determined by giving a numerical value to "x". For example, let's make x = 2, we get:

Therefore, the point (2, 5) is on the line. Now we plot the two points and join them with a line, like this: