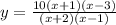Question

I have a question about rational functions in precalculus trigonometry picture included

Answer 1

Given the following parameters

`\begin{gathered} \text{Vertical asymptotes}\Rightarrow x=-2,x=1 \\ X-\text{intercepts}\Rightarrow x=-1,x=3 \\ \text{horizontal asymptote}\Rightarrow y=10 \end{gathered}`

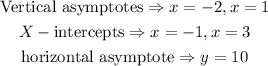
The vertical asymptotes indicates that denomenator will be (x+2)(x-1), i.e

`\begin{gathered} x=-2 \\ x+2=0 \\ x=1 \\ x-1=0 \end{gathered}`

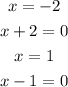
The intercepts on the x axis indicates that the numerator will be ( x+ 1) (x-3)

i.e

`\begin{gathered} x=-1\Rightarrow x+1=0 \\ x=3\Rightarrow x-3=0 \end{gathered}`

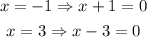
The equation would be in this form

`y=((x+1)(x-3))/((x+2)(x-1))`

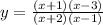
The equation above has a horizontal asymptote of y=1 as the degree of the numerator and denominator is equal , likewise their leading coefficient, i.e the ratio is 1:1

Thus, to make the equation have horizontal asymptote of y=10, multiply by 10/1

`\begin{gathered} y=(10)/(1)*\frac{(x+1)(x-3)}{(x+2)(x-1)_{}} \\ y=(10(x+1)(x-3))/((x+2)(x-1)) \end{gathered}`

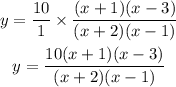
Hence, the rational function with the following parameters provided in the question is given by

`y=(10(x+1)(x-3))/((x+2)(x-1))`