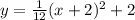For the parabola equation in standard form
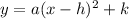
we know that the focus coordinate is
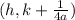
Since our focus is (-2,5), by comparing this coordinate with the last result, we can see that
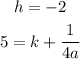
Then, the possible solution has the form
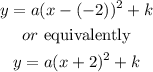
We can see tha the last option has this form. Lets corroborate that this is the correct choice. Then, we have that
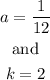
by substituting these values into the above equation:
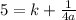
we have
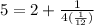
which gives
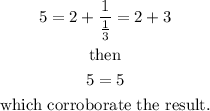
Therefore, the answer is the last option: