According to the law of conservation of momentum, we have
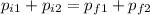
Where p = mv. So, using the definition of momentum, we have
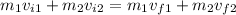
Let's use the given magnitudes and replace them with their letters.
![1,391\operatorname{kg}\cdot17.4((m)/(s))+1,280\operatorname{kg}\cdot v_(i2)=1,391\operatorname{kg}\cdot0+1,280\operatorname{kg}\cdot0]()
Observe that both final velocities are null because they come to stop. Let's solve for v.
![\begin{gathered} 24,203.4\operatorname{kg}\cdot(m)/(s)+1,280\operatorname{kg}\cdot v_(i2)=0 \\ 1,280\operatorname{kg}\cdot v_(i2)=-24,203.4\operatorname{kg}\cdot(m)/(s) \\ v_(i2)=\frac{-24,203.4\operatorname{kg}\cdot(m)/(s)}{1,280\operatorname{kg}} \\ v_(i2)\approx-18.91((m)/(s)) \end{gathered}]()
Therefore, the velocity of the second car before the collision is -18.91(m/s).
The negative sign shows that the second car is headed in the Western direction.