Question

Hi I got this wrong I don’t understand how to do

Answer 1

`r+3=-5+3r`

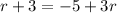
To solve for r, the objective is to isolate the variable on one side of the equation and all other terms on the other side.

- First, pass "3" to the right side of the equation by applying the opposite operation "-3" to both sides of the equal sign:

`\begin{gathered} r+3-3=-5-3+3r \\ r=-8+3r \end{gathered}`

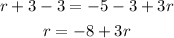
-Second, pass "3r" to the left side of the equation by applying the opposite operation "-3r" to both sides of it:

`\begin{gathered} r-3r=-8+3r-3r \\ -2r=-8 \end{gathered}`

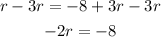
Third, the variable is being multiplied by "-2", to cancel this multiplication you have to apply the opposite operation, that is, divide the term by -2. And to keep the equality valid, you have to divide both sides.

`\begin{gathered} (-2r)/(-2)=(-8)/(-2) \\ r=4 \end{gathered}`

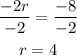
The result is r=4.