Use the laws of exponents to simplify the expression:

Use the first property to rewrite the expression in the denominator:
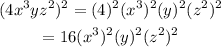
Use the second property to eliminate the parentheses:
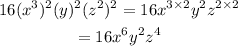
Rewrite the quotient using the new expression for the denominator:
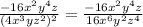
Use the fourth property to rewrite the quotient:
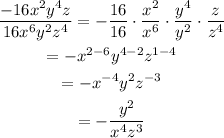
Therefore, the final answer is:
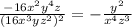
To simplify the quotient, the denominator was simplified squaring the expression inside the parenthesis and using the properties of the exponents to find the exponent of each variable. Then, the properties of exponents were used to simplify the quotient, performing the corresponding operations with each variable separately.