Given the table:
Let's compute the rate of change of temperature at all times in the table.
The time interval is 5 minutes.
To find the rate of change, apply the formula:
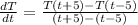
Where t is the time.
We have the following:
• When t = 5:
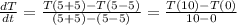
Where:
T(0) = 260.0
T(10) = 234.7
Thus, we have:

• When t = 10:
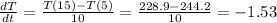
• When t = 15:
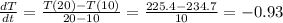
• When t = 20:
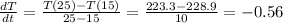
• When t = 25:
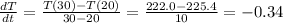
• When t = 30:
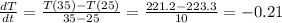
• When t = 35:
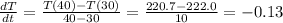
• When t = 40:

ANSWER:
AT t = 5: -2.53
At t = 10: -1.53
AT t = 15: -0.93
At t = 20: -0.56
At t = 25: -0.34
At t = 30: -0.21
At t = 35: -0.13
At t = 40: -0.08