Question

The midpoint of CD is M=(-1, -2) . One endpoint is C=(4, 3).Find the coordinates of the other endpoint, D.

Answer 1

We have a segment CD, of which we know the midpoint M = (-1,-2) and one of the endpoints C = (4,3).

We have to find the coordinates of the other endpoint D.

We will use the fact that the coordinates x and y of the midpoint are the average of the coordinates x and y of the endpoints respectively.

Then, for the x-coordinates we can write:

`\begin{gathered} x_M=(x_C+x_D)/(2)_{} \\ 2\cdot x_M=x_C+x_D \\ x_D=2x_M-x_C \end{gathered}`

Then, we can calculate the x-coordinate of D from the x-coordinates of C and M.

The same can be written for the y-coordinates:

`y_D=2y_M-y_C`

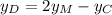
Then, we can replace and calculate each coordinate of D as:

`\begin{gathered} x_D=2x_M-x_C \\ x_D=2\cdot(-1)-4=-2-4=-6 \end{gathered}`
`\begin{gathered} y_D=2y_M-y_C \\ y_D=2(-2)-3=-4-3=-7 \end{gathered}`

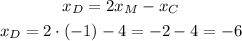
The coordinates of D are (-6,-7).

We can check with a graph as: