SOLUTION
Given the question in the image, the following are the solution steps to answer the question.
STEP 1: write the given values
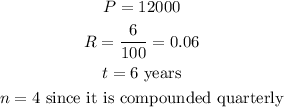
STEP 2: Write the formula for Amount
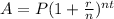
Where:
A=final amount
P=initial principal balance
r=interest rate
n=number of times interest applied per time period
t=number of time periods elapsed
STEP 3: Find the compounded amount
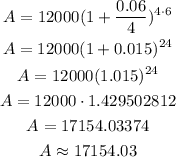
Hence, the amount after 6 years will be $17154.03