Question

X + 1/4y = 9X + y = 21Solve the equations algebraically

Answer 1

To solve the system of equations:

`\begin{gathered} x+(1)/(4)y=9 \\ x+y=21 \end{gathered}`

we first notice that both the x coefficients are equal, then we subtract the second equation from the first one to get an equation that only has y as a variable and we solve the resulting equation:

`\begin{gathered} (x+(1)/(4)y)-(x+y)=9-21 \\ (1)/(4)y-y=-12 \\ -(3)/(4)y=-12 \\ y=(-12)/(-(3)/(4)) \\ y=16 \end{gathered}`

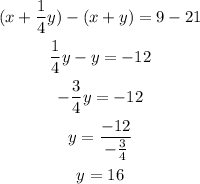
Once we know the value of y we plug it in the first equation and solve for x:

`\begin{gathered} x+(1)/(4)(16)=9 \\ x+4=9 \\ x=9-4 \\ x=5 \end{gathered}`

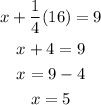
Therefore, the solution of the system of equations is x=5 and y=16