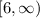Question

F(x)= (6x-36)^1/2 find the domain

Answer 1

`[6,\infty)`

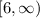
Step-by-step explanation

We want to identify the domain of the function:

`f(x)=(6x-36)^{(1)/(2)}`

Let us write the function:

`f(x)=√(6x-36)`

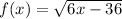
The domain of a function is the set of all x values for which the function is valid.

The given function contains a radical (square root). A radical is invalid if the radicand (the expression inside the radical) is less than 0.

This implies that the radicand must be greater than or equal to 0:

`6x-36\ge0`

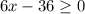
Now, solve for x:

`\begin{gathered} 6x\ge36 \\ \\ x\ge(36)/(6) \\ \\ x\ge6 \end{gathered}`

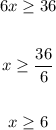
Hence, the domain of the function is:

`x\ge6`

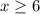
In interval notation, the domain is:

`[6,\infty)`