Question

Point R has coordinates (1, 3) and point S has coordinates (6, Y). If the distance from R to S is 13 units, what is the possible value of y?

Answer 1

To solve this, we will use the distance formula;

`|RS|=√((x_2-x_1)^2+(y_2-y_1)^2)`

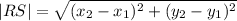
from the question;

RS = 13 x₁=1 y₁=3 x₂=6 y₂=y

substituting into the formula;

`13=\text{ }√((6-1)^2+(y-3)^2)`
`13\text{ = }√((5)^2+(y-3)^2)`

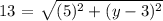
Take the square of both-side of the equation

`13^2=5^2+(y-3)^2`

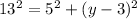
169 = 25 + (y-3)²

subtract 25 from both-side of the equation

144 = (y-3)²

Take the square root of both-side

`√(144)=y-3`

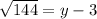
12 = y-3

add 3 to both-side of the equation

15=y

y=15