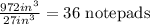1 Answer

Hoyland · Answer 1 · 2023-12-13T14:51:49+0000

The volume of each box is:

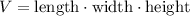
$V=\text{length}\cdot\text{width}\cdot\text{height}$

Substituting with length = 9 in, width = 9 in, and height = 12 in, we get:

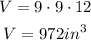
$\begin{gathered} V=9\cdot9\cdot12 \\ V=972in^3 \end{gathered}$

The volume of each notepad is:

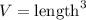
$V=\text{length}^3$

Substituting with length = 3 in, we get:

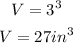
$\begin{gathered} V=3^3 \\ V=27in^3 \end{gathered}$

The number of notepads that fit in 1 box is obtained dividing the volume of the box by the volume of each notepad, as follows:

$(972in^3)/(27in^3)=36\text{ notepads}$

Please log in or register to add a comment.